Department of Radiation Oncology, Fox Chase Cancer Center, Philadelphia, PA 19111

Corresponding author: Chang-Ming Charlie Ma, Department of Radiation Oncology, Fox Chase Cancer Center, Philadelphia, PA 19111 Email: [email protected]

Copyright © 2019 Ma CM.

Citation: Ma CM. (2019). Physics and Dosimetric Principles of SRS and SBRT. Mathews J Cancer Sci. 4(2): 22

ABSTRACT

This paper reviews the radiation physics and dosimetric principles of stereotactic radiosurgery (SRS) and stereotactic body radiotherapy (SBRT). Recent radiation therapy physics and technology developments are reviewed followed by a brief description of the equipment available for SRS and SBRT. The treatment planning process and beam orientation optimization for SRS and SBRT are discussed. The dose calculation algorithms for radiation therapy are described including simple correction-based methods, advanced model-based algorithms and Monte Carlo simulations. Guidelines for SRS and SBRT treatment planning and plan evaluation are summarized including detailed dose prescription, organ dose tolerance and plan acceptance criteria. Finally, dosimetry measurements for SRS and SBRT are discussed with a focus on small field dosimetry.

Keywords: SRS, SBRT, dose calculation, Monte Carlo, treatment planning, dose prescription, organ dose tolerance, plan acceptance criteria, dosimetry measurement

INTRODUCTION

Radiation Physics and Technology Development

Stereotactic radiosurgery (SRS) is a precise radiation therapy technique, specially developed for the treatment of small tumors and functional abnormalities in the brain [1]. The physics and dosimetric principles of intracranial SRS, viz. high-precision, high-dose, focused radiation treatment, have also been applied to the treatment of extracranial tumors. This new treatment procedure is referred to as stereotactic body radiation therapy (SBRT).

Despite their names, SRS and SBRT are non-surgical procedures that deliver precisely-targeted, high-dose radiation in a single or very few fractions, as compared to conventionally-fractionated radiotherapy. SRS and SBRT are made possible with the advancement of medical imaging and radiation therapy technologies that allow maximum dose deposition in the treatment target while minimizing radiation damage to the surrounding normal tissue. The goal is to deliver a lethal dose to the tumor in order to achieve permanent disease control.

Physics and technological developments for SRS and SBRT

The development of SRS and SBRT is based on several radiation physics and technological advancements:

1. Three-dimensional imaging systems (e.g., CT and MRI) and localization techniques (e.g., a head frame) to determine the exact coordinates of the treatment target within the patient body.
2. Immobilization and positioning systems to maintain the patient treatment position during a therapy session.
3. Treatment optimization and delivery techniques to plan and deliver highly conformal dose distributions to the treatment target.
4. Image-guided radiotherapy (IGRT) to determine the location of the treatment target before and during radiation treatment.
5. Small field dosimetry that employs advanced detectors, devices, phantoms and measurement techniques to ensure the accuracy of SRS and SBRT dose delivery.

Historically, stereotactic surgery (or stereotaxy) is a minimally invasive form of surgical intervention that employs a three-dimensional (3D) reference coordinate system (such as a head frame) to locate tumors or abnormalities in the brain and perform some action on them e.g., biopsy, injection, implantation, stimulation, ablation, lesion and radiosurgery [2]. For extracranial sites, however, there are significant difficulties in establishing a reliable reference coordinate system that maintains a constant spatial relationship to bony structures or soft tissues. Thus, even though body frame systems have been developed and tested clinically for SBRT during its early clinical implementation, stereotaxy has predominantly been achieved using 3D imaging systems on modern SRS and SBRT machines. Advanced imaging modalities including CT, MRI, 2D/3D ultrasound and PET/CT have been used to locate treatment targets in the body. Multi-modality imaging is used in treatment planning to delineate the target volume and critical structures and in the delivery process to facilitate the precise positioning of the patient and real-time monitoring of the target during SRS and SBRT treatment sessions.

Although radiosurgery has commonly been referred to as a single-fraction treatment, it is sometimes necessary to perform a multiple-fraction stereotactic treatment, which is still ablative in nature. This is mainly for larger tumors because the normal tissue volume receiving high dose of radiation increases proportionally to the tumor size. Fractionated treatments will minimize damage to normal tissues by allowing time for repair, thus allowing for ablative doses to be delivered to the treatment target, while still maintaining a good safety profile. This procedure has been referred to as fractionated stereotactic radiotherapy (SRT), which is typically used to treatment large intracranial lesions in two to five fractions. SBRT generally refers to fractionated stereotactic radiotherapy for extracranial treatments. If the prescription dose is sufficiently high for an ablative treatment it is also referred to as stereotactic ablative body radiotherapy (SABR). For convenience, we will only use SRS for single fraction treatments and SRT/SBRT for multiple fraction treatments in this paper. In the United States, insurance companies set policies to reimburse single fraction SRS, and up to 5 fractions for SRT/SBRT, which were not based on radiation physics, radiobiology or clinical efficacy.  

SRS and SBRT equipment

Commonly used SRS and SBRT machines can be classified into three categories based on the radiation sources used:

1. Gamma ray systems: The Gamma Knife® system uses 192 or 201 cobalt sources all aiming at the treatment target [3]. Other designs have used 30 rotating cobalt sources to achieve smooth focal dose distributions [4]. Gamma ray systems are ideal for SRS and SBRT for small tumors. Novel designs using multiple rotating gamma sources and image guidance are available for clinical applications of both intracranial and extracranial sites (the CybeRay system) [5].
2. Linear accelerator (Linac) systems: Clinical Linacs have received widespread radiotherapy application in the world [6]. A Linac machine can perform single-fraction SRS for small lesions using cone collimators or multiple-fraction SBRT for larger tumors using MLC collimators. Several manufacturers provide Linac-based SRS and SBRT machines, e.g., CyberKnife®, XKnife™, Novalis Tx™, Axesse™ and Edge^TM. A hybrid machine combing a focusing cobalt head and a Linac-MLC head has been reported recently [7].
3. Proton or heavy-charged-particle systems: Although a growing number of proton centers have been established in the last several years [8] the use of proton or heavy-charged-particle beams for SRS and SBRT remains in limited application worldwide. It is less cost-effective to perform a SRS/SBRT treatment using proton beams than using gamma and x-rays.

Treatment planning and optimization for SRS and SBRT

Unlike conventional radiation therapy, which delivers a uniform dose to the entire target volume, the dosimetric requirements for SRS and SBRT are different in two aspects: (1) a small target volume, containing the gross tumor and its close vicinity, is treated with a very high prescription dose per fraction and heterogeneous dose distributions (e.g., hotspots) within the treatment volume are considered to be acceptable [9]; and (2) the normal tissue volume outside the treatment target that receives high doses is minimized to reduce the risks of treatment toxicity, which requires a steep dose fall-off away from the target [9].

Definition of Target Volume and Critical Structures

Radiation therapy is a localized treatment. The success of radiation therapy depends on the precise knowledge of the treatment target and the surrounding critical structures. To define the treatment volume(s) for SRS and SBRT, the location and extent of the disease including subclinical and microscopic tumor extension must be characterized. Various imaging modalities, and help and advice from diagnostic specialists are therefore crucial for radiation therapy planning.

Three main volumes have been defined for radiation therapy treatment planning [10]:

1. The gross tumor volume (GTV): This is the gross tumor that can be seen or palpated. At the present time, GTV is mainly determined using various imaging modalities.
2. The clinical target volume (CTV): This is a volume containing the GTV and an appropriate margin for subclinical and microscopic disease that usually cannot be detected by imaging. It is difficult to determine the CTV accurately, mostly based on clinical experience, for a particular patient, but it is necessary to treat the CTV adequately to achieve disease control.
3. The planning target volume (PTV): This is a volume containing the CTV and a safety margin, accounting for random and systematic uncertainties in treatment planning and dose delivery. It is a geometric concept designed to ensure that the CTV actually receives the prescription dose.

For some body sites that are affected by respiratory motion, such as a lung tumor or a liver tumor, an internal margin is added to the CTV to compensate for internal physiologic movement and variations of the tumor in position, shape and size. This is referred to as internal target volume (ITV). Four-dimensional computed tomography (4DCT) is currently being used to obtain the ITV either by delineating the target volumes on CT images at 10 breathing phases or on a single maximum intensity projection (MIP) image. Early studies showed that the ITV could be estimated by combining target volumes drawn on CT images at the end of expiration and that at the end of inspiration (a poor man’s ITV). An isotropic 5mm ITV-PTV margin has been used by many institutions for Linac-based lung SBRT with 4D imaging [9]. For most cases, however, this margin should be determined based on the equipment used and the institutional experience with SRS and SBRT.

An important goal of treatment planning is to avoid radiation damage to critical organs and normal structures, known as organs at risk (OARs). OARs are delineated, and in some cases, a safety margin is added around an OAR to account for the random and systemic uncertainties. This is referred to as a planning OAR volume (PRV). It is useful to apply the PRV concept for some critical organs such as the spinal cord in SRS and SBRT planning, in which higher-than-safe exposures to a small fraction of the OAR (e.g., a serial organ) may cause a severe clinical manifestation. GTV, CTV, ITV, PTV, OAR and PRV are very important concepts in SRS and SBRT treatment planning, which can affect clinical outcomes.

In principle, the delineation of the GTV and CTV should be independent of the treatment techniques, be it SRS, SBRT or conventional radiation therapy. For the delineation of volumes, and in their use, it is irrelevant whether gamma rays, x-rays, protons, or any other radiation is to be employed. It is important not to let the intended treatment modality affect how these volumes are delineated. Consistent target and OAR determination is a key requirement to combine, compare, or retrospectively analyze treatment plans for more than one treatment modality.

Regarding the PTV margin, AAPM TG101 report stated that at the present time, it is difficult to determine target margins based on clinical results directly [9]. For SRS and SBRT planning, target margins should be determined based on the in-house immobilization and localization techniques used and the random and systematic treatment uncertainties associated with the disease site for an individual patient. Accordingly, systematic efforts should be made to gain clinical experience and establish margin recipes for future applications.

Treatment plan optimization

The dose delivery techniques for SRS and SBRT can be 2D conventional, 3D conformal radiation therapy (3DCRT), dynamic conformal-arc therapy, intensity-modulated radiotherapy (IMRT) and volumetric-modulated arc therapy (VMAT). Modern commercial treatment planning systems (TPS) that can plan for SRS and SBRT have implemented advanced optimization algorithms. Detailed descriptions of optimization algorithms for special delivery techniques, e.g., IMRT and VMAT, are beyond the scope of this review. However, beam orientation is still an important factor for a planner to consider in the SRS and SBRT planning process.

The goal of beam orientation optimization in SRS and SBRT planning is to avoid sensitive organs and to select short beam paths whenever possible. Mechanical constraints and collision risks imposed by the equipment must be considered. Generally, more radiation beams lead to more conformal target dose distribution and more isotropic dose gradient outside of the target volume, especially for centrally located targets. When an SBRT plan contains a sufficient number of beams, the choice of beam orientation becomes insignificant. However, for shallow or irregularly shaped targets, multiple-angle IMRT may still be preferable. It is generally desirable to keep the entrance dose as low as possible (e.g., <30% of the accumulative dose) to prevent acute skin reactions. This can be achieved by avoiding overlapping beams and maintaining an isotropic dose fall-off. Higher energy photon beams (e.g., 10 MV vs. 6 MV on a Linac) are more suitable for larger patients to reduce peripheral doses, especially for treating abdominal and pelvic targets. However, this difference diminishes when a sufficient number of beam angles is used (the advantages of rotational arc therapy).

Mechanisms for beam orientation optimization to minimize dose deposition in normal tissue have been investigated. Rotational therapy such as VMAT is generally superior to its static field counterparts in producing conformal dose distributions to cover the target, spare critical structures, and reduce treatment times. In many cases, a uniform dose fall-off with VMAT is desirable, but in some cases the treatment target is in close proximity to one or more critical structures, a sharper dose fall-off may be required in some particular directions, which may be achieved by selecting more perpendicular beam angles. When treating paraspinal tumors with SBRT, for example, the target volume usually contains the vertebral bone and/or attached soft-tissue tumor growth, which is immediately adjacent to the spinal cord. An isotropic dose fall-off around the treatment target, typically achievable with VMAT, may exceed the dose tolerances for the cord. An IMRT plan with 9-11 carefully selected beam angles may generate a sharper dose fall-off of >10%/mm between the spinal cord and the target, adequately delivering >90% of the prescription dose to the PTV while sparing the cord.

Dose calculation

An important physical quantity in radiotherapy dosimetry is Absorbed Dose (D), which is defined as the energy imparted by ionizing radiation per unit mass of medium (unit of D: gray or Gy; 1Gy = 1J/kg). The accuracy of absorbed dose calculation is critical in radiation therapy treatment planning, while dose calculation algorithms are instrumental in the treatment planning process.

There are three types of dose calculation algorithms that are commonly used in TPS:

1. Correction-based algorithm: This is a semi-empirical approach to account for tissue inhomogeneity and surface contour variation based on standard dose distributions in water.
2. Model-based algorithm: This approach computes dose distributions in a phantom or a patient by integrating the energy fluence with a dose kernel.
3. Monte Carlo algorithm: This method calculates dose distributions by directly simulating particle transport and energy deposition in the phantom or patient geometry [11].

Correction-based algorithm

Correction-based algorithms were widely used in conventional radiation therapy, which involved minimal computation. There are generally two steps in dose calculation using a correction-based algorithm:

(1) Establishing dose calculation data;

(2) Reconstructing patient dose distribution by applying corrections.

Establishing Dose Data Library

The basic dose data (or dose data library) can be measured in water under some standard conditions including a fixed source-to-surface distance (SSD) and normal beam incidence. The water phantom has to be large enough in volume to provide full electron equilibrium.  The dose measurements under those conditions include:

• Central-axis depth doses for various square or circular fields, normalized to the maximum value.
• Lateral dose profiles at various depths, normalized to the central axis value, extended outside of the open field, which are also referred to as off-axial ratios (OAR).
• Beam output factors for various square or circular fields, relative to a reference field (typically 10x10 cm²), which are further separated as phantom-scatter factors, S_p, and collimator-scatter factors, S_c.
• Beam modifier factors (f) for various field sizes and depths to account for the attenuation and scattering effect of beam modifiers, e.g., a wedge, a compensator or a beam spoiler.

Another dose quantity used in early-stage radiotherapy is the tissue-air ratio (TAR). This is the ratio of the dose to water at a point in water to dose to water at the same point free in air. For beam energies above 4 MV, it becomes impractical to measure TAR (the real difficulty is to determine dose to water free in air). A more practical dose quantity, the tissue-phantom ratio (TPR), is used for megavoltage photon beams, which is defined as the ratio of dose to water at a depth in water to that at a reference depth. If the reference depth is set to the depth of the maximum dose in water, this ratio is referred to as tissue-maximum ratio (TMR). TMR is a dose quantity widely used clinically, especially for SAD (source-axis distance) treatment techniques.

Theoretically, the dose in a photon field that satisfies the above standard conditions can be calculated using the following equation:

Where, MU is the monitor chamber reading of a Linac (or the beam-on-time of a cobalt unit) and C is the machine calibration factor, which specifies the dose received at a reference point for a monitor unit (MU) (or a unit of beam-on-time). This equation is still widely used by medical physicists to perform a “hand calculation” to check dose contribution for a given MU, or the MUs needed for individual beams of a treatment plan for a given prescription dose, using the SAD technique.

However, the situations encountered in clinical radiotherapy often impose limitations on the use of “standard” distribution functions and dose calculation parameters. Therefore, various correction methods have been used under nonstandard conditions.

Reconstructing Dose Distribution

Correction for Irregular Fields

Photon scatter contributions can be estimated using the Clarkson method by summing up or integrating the individual scatter contributions of each decomposed fan beamlet, i.e., a small sector of the irregular field [12].  The dose at a point in an irregular field is calculated from the primary and scattered components using an effective TMR, that is:

                                                                                         (2)

where TMR(0,d) is the primary photon component and SMR(d,r) is the scatter maximum ratio at depth d for a fan beamlet with a radius  r_i, which is calculated as the ratio of the scattered dose at the point to the effective primary dose at the same point at the depth of maximum dose.

Correction for Surface Irregularities

A convenient, yet effective method to make contour corrections to account for beam oblique incidence or surface curvature is the TMR method. Since TMR only depends on the depth and the field size at the depth, not SSD, thus, the surface contour correction factor (CF) will be

                                                                                                                        (3)

Where, r_P is the projected field size at P (i.e., at the distance of SSD + d).

The corrected dose D_c at P is thus given by:

                                                                                                                                   (4)

Where, D is the uncorrected dose. 

Correction for Tissue Heterogeneities

Traditionally, the effects of tissue heterogeneities are corrected using semi-empirical methods, such as the TAR method. The key to this correction is to employ an effective depth by scaling the physical depth using the relative electron density (with respect to that of water).  The physics principle for this method is that, for high-energy photon beams, the dominant mode of interaction is Compton Effect, which results in beam attenuation and photon scattering in any tissue scalable with electron density. Thus, the heterogeneity correction factor is defined as

                                                                                                                            (5)

where r_d is the field size projected at P, d the actual depth of P from the surface and d_e is the equivalent water depth.

Another improvement was to predicate scattered dose by scaling the field size using relative electron density.  The heterogeneity correction factor based on the “equivalent” tissue-air ratio (ETAR) is

                                                                                                                              (6)

where r_e is the equivalent field size scaled by the weighted average density of the heterogeneities.

Model-based algorithm

Deterministic model-based algorithms such as the convolution-superposition method have been developed and implemented clinically in various forms. The common feature of these algorithms is the use of dose kernels to model dose distributions resulting from interactions of primary radiation particles at a point or along a ray line in the dose calculation geometry. Generally, dose kernels at different locations in a human body should not be the same due to the existence of various tissue compositions and densities. For efficiency, however, simplified dose kernels have been used in commercial TPS. Thus, the accuracy of a convolution-superposition algorithm depends critically on how the kernel variation is implemented for heterogeneous geometry. 

Convolution-Superposition with Point Dose Kernels

Mathematically, for a monoenergetic photon field, the dose  at a point (a vector that consists of x, y, z component, i.e.  ) is given by:

                                                                                                                                (7)

where μ/ρ is the mass-energy attenuation coefficient,   the primary energy fluence, and  the point-dose kernel. The point dose kernel is the dose distribution by primary photon interactions at a point in water (including contributions from both scattered photons and secondary charged particles). The product of mass-energy attenuation coefficient and the primary energy fluence has been referred to as TERMA, the total energy released per unit mass. 

Since the primary energy fluence and point-dose kernels are functions of energy, the total dose can then be calculated by integrating TERMA with the point dose kernel over the energy spectrum. 

The Fast Fourier Transform (FFT) Algorithm

Dose calculation in homogeneous geometry using Eq. 7 can be performed very efficiently with the FFT method. The convolution of two functions with three variables each in the physical space can be transformed into the product of the two functions in the frequency space. The FFT method is similar to correction-based algorithms in accuracy for heterogeneous geometry because it ignores the spatial variation of the point dose kernel completely.

The Superposition Algorithm

When dose calculation is performed in heterogeneous geometry, the point dose kernels vary spatially and the dose at a point has to be summed up by superposition of the variable point dose kernels, which are typically approximated by stretching or compressing the point dose kernel based on the electron density of the local medium. Mathematically, the dose at a point (i,j,k) is given by

                                      (8)

Where,   represents the scaled point dose kernel based on local electron density. The point dose kernels can be represented in a Cartesian grid or discretized using collapsed cones [13]; the latter are more computationally efficient (e.g., for kernel tilting and density scaling). It is also more efficient to separate the point dose kernel into a primary kernel for secondary charged particles and a scatter kernel for scattered photons with a different spatial resolution. Due to kernel scaling, the superposition method is more accurate and time-consuming than the FFT convolution method for heterogeneous geometry.

Convolution-Superposition with Pencil-Beam Dose Kernels

The pencil-beam dose kernel is the dose distribution from a single ray of primary photons (i.e., dose contributions resulting from scattered photons and secondary electrons).  The dose distribution can be calculated by

 

                                     (9)

Where, 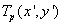  is energy-integrated TERMA at the patient surface, and  is the pencil beam dose kernel. 

For heterogeneous geometry, the depth coordinate z is scaled by electron density, which means the pencil-beam kernel is stretched or compressed longitudinally. The effect of lateral density variation from the considered ray is ignored or approximated using the ETAR correction (Eq.6). This places the pencil-beam algorithm in the category of correction-based dose algorithms. 

The Finite-Size Pencil-Beam (FSPB) Algorithm

In FSPB, the dose kernel is a 3D dose distribution resulting from a photon beam of a finite field size that typically corresponds to a beamlet used in IMRT or VMAT. The advantage of FSPB is its high computation efficiency, as the convolution-superposition is performed in two dimensions, which is essential to pre-optimization dose calculations when hundreds or even thousands of beamlets are needed to achieve an optimal dose distribution. However, due to its approximation in heterogeneity correction, FSPB algorithms may show significant uncertainties at the vicinity of heterogeneities. Therefore, more accurate dose algorithms (e.g., convolution-superposition or collapsed-cone methods) are often used in the post-optimization dose calculation for advanced treatment techniques.

The Anisotropic Analytical Algorithm (AAA) Algorithm

The AAA algorithm in the Varian Eclipse TPS is an improved pencil-beam algorithm, which uses multiple pencil-beam dose kernels to describe the dose contributions from various radiation sources of a clinical beam. In particular, the pencil-beam dose kernels for the photon sources are further separated into a depth component and a lateral component.  The heterogeneity correction is incorporated in the dose summation stage by scaling the depth dose component using the equivalent path length and the lateral component anisotropically according to local electron density. This has significantly improved its accuracy for heterogeneous geometry compared to other pencil-beam algorithms. Varian Eclipse TPS also implemented a photon dose calculation algorithm called Acuros XB (AXB), which is based on the solution of the Linear Boltzmann Transport Equation (LBTE). AXB uses the same source model and commissioning beam data as the AAA algorithm but it is more efficient for RT plans with more beam angles such as VMAT.

Monte Carlo Simulations

The Monte Carlo method is theoretically the most complete and rigorous dose-calculation method, since it simulates the radiation transport and energy deposition of individual particles following the fundamental laws of physics.  In fact, it is the only method that takes into account electronic disequilibrium at medium interfaces and in tissue heterogeneities, as well as particle backscattering from dense materials such as teeth, bones and metal prostheses in a patient. 

Monte Carlo dose calculation consists of using a computer program to simulate the transport and interaction of individual particles in a patient by random sampling from probability distribution functions that govern the underlying physical processes. The patient’s geometry is reconstructed from CT data with different biological media and mass densities. The dose distribution is calculated by tallying the ionization events that give rise to energy deposition in individual calculation voxels.  In order to obtain statistically meaningful dose distributions, a large number (>10⁸) of radiation particles have to be simulated for a radiation treatment, resulting in long CPU times. This situation has been improved with the availability of fast computers and various variance-reduction and efficiency-improvement techniques such as photon interaction forcing, particle splitting, Russian roulette and electron track repeating.

Accurate Monte Carlo dose calculation requires the precise knowledge of the phase-space information (i.e., the angle, position and energy) of the radiation particles impinging on the patient. This can be achieved by directly simulating the radiation beams from the clinical accelerator or using source models with parameters derived from measurements or Monte Carlo simulated phase space data [14]. Patient-specific beam modifiers such as wedges, blocks and multileaf collimators can be directly simulated in the patient dose calculation to account for their attenuation and scattering effects.

Currently, Monte Carlo dose calculation has been used extensively for assessing existing dose calculation algorithms, investigating novel treatment modalities and treatment techniques prior to their widespread clinical applications, and validating treatment dose delivery in combination with advanced image guidance and in vivo dosimetry measurements [15]. Several commercial treatment planning systems have implemented Monte Carlo algorithms for advanced radiotherapy treatments [16,17]. Monte Carlo algorithms are expected to be the dose engine for the next generation of TPS.

Recommendations on heterogeneity dose calculations

Heterogeneity correction is important to treatment planning for lung and head-and-neck cancers, in which the effects of charged particle disequilibrium and lateral electron scattering in low-density tissue may result in a significant reduction in the target dose especially at the target boundary. Up to 20% target dose reductions have been observed in lung SBRT cases. Simple correction-based dose algorithms that do not consider lateral charged particle scattering can produce incorrect dose distributions.

Many commercial TPS available for SRS and SBRT have implemented model-based dose algorithms that employ dose spread kernels precalculated by Monte Carlo and convolution-superposition techniques. Although these model-based dose algorithms consider the effect of secondary electron transport, only approximate methods are used to account for the heterogeneity effect. For example, the pencil-beam superposition algorithm does not account properly for variations of electron scattering in lower-density tissues. For those methods that use point dose spread kernels, ray tracing of the radiological distance from the interaction to the dose calculation point is performed for density scaling, which assumes that charged particles travel in straight lines or assuming no effects from non-straight paths.

The accuracy of inhomogeneity corrections for SRS and SBRT small-field dosimetry has been investigated. The Imaging and Radiation Oncology Core (IROC) Houston QA Center (previously RPC) presented dose comparisons of various dose calculation algorithms used by different hospitals participating in the Radiation Therapy Oncology Group (RTOG) lung SBRT (0236) trial using an anthropomorphic thorax phantom. Both correction-based and model-based algorithms predicted the dose accurately at the target center. However, significant differences were found in the peripheral regions surrounding the target. AAPM TG 65 report recommended the use of inhomogeneity corrections for treatment planning dose calculations, and the potential pitfalls of several heterogeneity correction algorithms in commercially available TPS were discussed for various clinical scenarios [18]. AAPM Task Group 65 specifically disallows the pencil-beam algorithm for situations, in which the target volume is surrounded by low density tissue such as in lung SBRT.

It is generally accepted that model-based algorithms such as convolution-superposition are adequate for most SRS and SBRT applications, where there exists charged particle disequilibrium at the lung-tissue/bone-tissue interface or target margin in a low-density medium. Dose algorithms perform precise particle transport, e.g., Monte Carlo is favorable for the most demanding clinical situations, and for example, a small tumor is surrounded completely by low-density lung tissue. Currently, Monte Carlo dose calculation has been implemented clinically and some commercial systems have included Monte Carlo dose calculation for SRS and SBRT applications, for example, the Accuracy CyberKnife TPS [17] and the Elekta Monaco system [19]. SRS and SBRT treatment planning for lung and head and neck should not use pencil-beam algorithms for dose calculation.

Recommendations on voxel size

The dose calculation voxel size (or grid resolution) in treatment planning dose calculation may affect the dose computation results. Studies show that a 2.5 mm uniform grid results in a 1% dose calculation accuracy in the high-dose region for highly modulated IMRT plans [20] while a 4 mm grid resolution deteriorated the dose to 5% [21]. It is reported that a 2.3% dose difference can be seen between 2 mm and 1.5 mm grid resolution, rising to 5.6% for a grid resolution of 4 mm. Thus, 2 mm grids are necessary for SRS and SBRT dose calculation, especially for small dose dimensions and sharp dose fall-offs [22]. Since SRS and SBRT dose distributions commonly include highly variable doses inside the target and sharp dose fall-offs outside of the target and often utilize sophisticated delivery techniques, it has been recommended to use a uniform grid resolution of 2 mm or smaller. Larger (≥ 3 mm) grid sizes are discouraged for SRS and SBRT dose calculation [9].

Dosimetric Considerations for SRS/SBRT Planning

Target Dose Heterogeneity

For SRS and SBRT the prescription dose is often specified at lower isodose, e.g., 50% for SRS and 60%-80% for SBRT, as recommended by the AAPM and ASTRO [9,23]. This is because the dose gradient between 40-80% isodose lines is much greater than that between 85-95% isodose lines. For conventionally fractionated radiotherapy, the dose prescription is specified at 85-95% isodose, which results in better target dose uniformity. The dose fall-off outside of the target is usually slow but this is acceptable with conventional dose fractionation. Because of the ablative nature of SRS and SBRT, sharper dose fall-offs outside of the treatment target is required to avoid damaging nearby OARs. Thus, the prescription dose is specified to lower isodose lines; the selection of 50-80% isodose for dose prescription is a compromise between dose fall-off and target dose heterogeneity. This practice results in much higher dose heterogeneity within the treatment target in comparison with the practice in conventional fractionation. High dose heterogeneities within the target volume are acceptable for SRS and SBRT plans if the target volume does not contain functional normal tissue. AAPM TG101 report states that hotspots within the central region of a tumor might offer a special advantage in eradicating radioresistant/hypoxic cells that might be more likely located in that area. Higher doses inside the treatment volumes can be desirable, provided that hotspots are within the target. This recommendation is supported by observations of dose response for tumor control in early clinical SRS and SBRT trials [9].

Dose Gradient

Similar to planning for intracranial SRS, it is very effective to use as many non-overlapping beams as possible to achieve a sharp dose fall-off around a small target in SBRT planning. Unless there are critical structures such as the spinal cord or a rib immediately adjacent to the treatment target, the dose outside the target volume should fall off uniformly. This can be achieved using many beams focusing on the target like the GammKnife system or using rotational delivery like dynamic conformal arc or VMAT on a Linac.

Two major factors affect the dose gradient outside of the treatment target. One is the beam energy; the beam penumbra is broader for higher beam energies because of secondary electron scattering in a medium. This effect is more significant for lower density tissues, such as lung. For SRS and SBRT lung applications, 6 MV photon beams, available on most modern Linacs, can be used, which is a reasonable compromise between the beam penumbra characteristics and depth penetration [9]. Recent developments of image-guided rotational gamma-ray systems (CybeRay, OUR United RT Group, Beijing, China) have shown great potential for SRS and SBRT [24]. Small-source cobalt beams have sharp penumbra and rapid depth dose falloff, which are ideal for peripheral lung tumors with partial-arc deliveries to spare nearby critical structures and the opposite lung. The other is the leaf geometry of the MLC. Partial transmission through the rounded leaf ends and the tongue and groove structure increases the beam penumbra. In general, finer MLC leaves improve the conformity of the MLC field with respect to the cross-section of the target volume. Because of the finite source size and secondary electron lateral scattering, however, negligible improvements have been found for very small MLC leaf width (3 mm or smaller) except for very small lesions [25]. The 5 mm MLC leaf width available on most modern Linacs is adequate for most SBRT applications. Small tumors may be better treated with small cone collimators, which have narrower beam penumbra than MLC.

Dosimetric Parameters for Plan Evaluation

Many dosimetric parameters are used in SRS and SBRT plan evaluation. Tight target dose conformality is an important requirement for SRS and SBRT. This is usually obtained using multiple, non-overlapping, and sometimes non-coplanar beams or arcs, spread in a large solid angle with fairly equal weighting to minimize the entrance dose and ultimately the volume of intermediate dose. Another important clinical factor is the entrance dose, which should be kept to a modest level to prevent potential severe skin or chest wall toxicity. This can be achieved by optimize the number of beam directions and the relative beam weights for SRS/SBRT planning. If the beam’s eye-view of each radiation field coincides with the cross-section of the PTV (i.e., with no block margin or a 1-2mm block margin), less surrounding normal tissues will be exposed to direct radiation fields. The resulting dose distribution can be normalized by specifying the prescription dose to a lower isodose line, e.g., 60% to 80%, to provide 95% PTV coverage. For conventionally fractionated radiotherapy, a 4-6 mm block margin will be used so that a prescription isodose line of 85-95% can be used to cover the PTV with a more homogeneous target dose distribution.

Target dose coverage:  The target dose is normalized to prescribe the dose to either 50% isodose for intracranial SRS or 60-80% isodose for SBRT to achieve a 95% or higher coverage of the target volume. This results in a D_max up to 200% of the prescription dose for SRS or between 130-170% of the prescription dose for SBRT, which must be inside the PTV. Another important target dose requirement is at least 99% of the PTV should receive more than 90% of the prescription dose (i.e., allowing a cold spot of <10%).

In assessment and evaluation of SRS and SBRT plans, three major criteria are recommended by ASTRO: conformity index, high dose spillage, and intermediate-dose spillage [23]. These concepts have been used in RTOG multicenter SBRT trials. The target dose requirements and OAR constraints as a function of structure volume can be found in the radiotherapy sections of these protocols (e.g., RTOG 0236, 0618, 0813 and 0915, etc).

Conformity index (CI):  The  conformity index is defined  as  the  ratio  of  the  volume  of  the  isodose  shell  that  receives the prescription dose (TV100%) to  the PTV volume (CI = TV100%/PTV).  It is recommended that this ratio be kept to less than 1.2 to minimize the volume of tissue receiving an ablative dose. Greater CI (e.g., up to 1.5) may be used for small tumors (<2.5cm).

High-dose spillage: Any areas receiving greater than 105% of the prescription dose, commonly referred to as high-dose spillage, are generally confined to the PTV. For difficult cases, normal tissue volume receiving >105% of prescription dose should be kept under 15% of the PTV.

Intermediate-dose spillage: Intermediate-dose spillage is responsible for most of the toxicity associated with SRS and SBRT if the target volume is adjacent to critical organs or structures. This can be evaluated using one or both the following methods: (1) to keep dose to any point 2cm away from the PTV surface (D2cm) below a limit, and (2) to keep the ratio of 50% isodose volume (TV50%) to the PTV volume (R50% = TV50%/PTV) as low as possible. For example, try to keep R50% under 5 for large targets (>4cm in any direction) or under 8 for small tumors (<2cm in any direction).

Target Dose Prescription and Critical Structure Dose Constraints

SRS and SBRT treatments have garnered great interest in the last decades and various dose/fractionation schemes have been adopted in clinical trials and used for routine clinical treatments. At the time of writing, there have been no sufficient clinical outcome data to determine the best dose prescription/fractionation or precise dose constraints for various treatment sites and critical organs/structures. Presently, single-fraction SRS is primarily used for intracranial tumors and spine lesions while multiple-fraction SBRT is often used for other treatment sites. Generally smaller target volumes will allow for fewer fractions of large doses while for large tumor volumes especially when they are adjacent to critical structures more fractions will be needed to reduce normal tissue toxicities. Below are typical target dose prescriptions used in clinical trials and our institution for various body sites.

Brain: For brain metastases, with median minimum peripheral doses of 16.5-25Gy, a 70-95% local control rate can be expected. Up to 5 lesions can be treated at one time. A whole brain irradiation (WBI) of 30-40Gy at 2Gy/fraction can be given before or after the SRS treatment, However, recent studies have shown a single SRS treatment without WBI may result in better survival and neurocognitive function. Prescription doses for other diseases: SRS 16.5-20Gy for AVM; SRS 15-20Gy and SRT 45-50Gy for pituitary adenoma; SRS 10-12.5Gy and SRT 20-25Gy for acoustic schwannomas (neuromas); SRS/SRT 10-50Gy for meningioma; SRS 12-17Gy before or after RT for GBM; SRS/SRT 70Gy for trigeminal neuralgia, 120-180Gy for thalamotomy, and 120-160Gy for pallidotomy. 

Spine: Various prescription doses have been used: for example, UPMC: SRS a single mean dose of 16.31Gy; Georgetown Univ.: SBRT 20.59Gy in 3 fractions; FCCC: SRS 16-18Gy and SBRT 24-30Gy in 3-6 fractions.

Lung: Prescription dose for lung SBRT depends on tumor size and location. In our institution we typically prescribe 48Gy in 4 fractions for peripheral tumors >2 cm from the primary bronchial tree; 50Gy in 5 fractions for central tumors or large tumors adjacent to chest wall or rib; 50Gy in 5 fractions for isolated recurrence after conventional RT in a potentially curable patient; and 40-50Gy in 5 fractions for oligometastatic disease. The latest NCCN clinical practice guidelines for non-small cell lung cancer (version 3.2019, available at NCCN.org) listed SBRT dose prescription: 25-34Gy single fractions for peripheral, small (<2cm) tumors, especially >1cm away from the chest wall; 45-60Gy in 3 fractions for peripheral tumors >1cm from the chest wall; 48-50Gy in 4 fractions for central or peripheral tumors, <4-5cm, especially >1cm from the chest wall; 50-55Gy in 5 fractions for central and peripheral tumors, especially >1cm from chest wall; and 60-70Gy in 8-10 fractions for central tumors. 

Liver: Prescription dose for liver SBRT varies drastically in various clinical trials, for example, 15-45Gy in 1-5 fractions for primary and metastatic disease [26]; 36-60Gy in 3 fractions for one to three hepatic metastatic lesions [27]; 60Gy in 5 fractions [28]; 45-62Gy in 3 fractions for hepatic metastases [29]; and 37Gy in 5 fractions for hepatic metastases [30]. At FCCC, we typically treat hepatic metastases from colorectal cancer (CRC) with 60Gy in 5 fractions, and hepatocellular carcinoma (HCC) with 50Gy in 5 fractions, or 40Gy in 5 fractions (possible 3 fractions of 8Gy, one month break and then 2 fractions of 8Gy).

Prostate: New ASTRO/ASCO/AUA guidelines suggest moderate hypofractionation (2.4-3.4Gy/day) as an alternative to conventional fractionation (1.8-2 Gy/day), for example: 60Gy in 20 fractions or 70Gy in 28 fractions. Ultra-hypofractionation (≥5Gy/day) may be offered to low-risk patients as an alternative, but only through clinical trials for intermediate-and high-risk patients, for example: 35Gy in 5 fractions or 36.25Gy in 5 fractions (consecutive days). The RTOG trial 11-074 prescribes 37Gy in 5 fractions (2 fractions per business week).

Pancreas: SBRT trials have been designed to treat pancreatic cancers to increase the likelihood of surgical resection and therefore prolong patient’s survival. Various dose schemes have been used including 15-25Gy in a single fraction [31,32], 24-45Gy in 3 fractions [33-35] and 25-33Gy in 5 fractions [36,37]. At FCCC, we typically prescribe 25-37Gy in 5 fractions.

Although there are variations of dose/fractionation schemes for a particular body site, the actual dose/fractionation for an individual patient may be affected by the potential normal tissue toxicities. Tables 1 to 5 list the volume-dose constraints and the maximum point dose limits for various organs and normal tissues for single-fraction SRS and multiple-fraction (e.g., 3, 4, 5 and 8) SBRT treatment planning. The dose tolerance values in these tables are based on the RTOG protocols and data in the literature [38,39], which have been used in our institution as a planning guide.

Table 1: Volume-dose constraints and the maximum point doses (volume <0.035cc) for various tissues/organs for a single-fraction SRS treatment. Circumferential irradiation should be avoided for tube-like organs such as esophagus, bronchus, duodenum, jejunum/ileum, colon and rectum.

Tissue/Organ	Volume	Volume Max Dose	Max Point Dose
Optic pathway	<0.2 cc	8 Gy	10 Gy
Cochlea			9 Gy
Brainstem (not medulla)	<0.5 cc	10 Gy	15 Gy
Spinal cord and medulla (10cm above and below treatment target)	<0.35 cc <1.2 cc	10 Gy 8 Gy	14 Gy
Spinal cord subvolume (5-6mm above and below treatment target)	<10%	10 Gy	14 Gy
Cauda equina	<5 cc	14 Gy	16 Gy
Sacral plexus	<5 cc	14.4 Gy	16 Gy
Esophagus	<5 cc	11.9 Gy	15.4 Gy
Brachial plexus	<3 cc	13.6 Gy	16.4  Gy
Heart/pericardium	<15 cc	16 Gy	22 Gy
Great vessels	<10 cc	31 Gy	37 Gy
Trachea and large bronchus	<4 cc	17.4 Gy	20.2 Gy
Bronchus- smaller airways	<0.5 cc	12.4 Gy	13.3 Gy
Lung (right & left)	1500 cc	7 Gy
Lung (right & left)	1000 cc	7.6 Gy	V8Gy <37%
Rib	<5 cc	28 Gy	33 Gy
Skin	<10 cc	25.5 Gy	27.5 Gy
Stomach	<5 cc	17.4 Gy	22 Gy
Bile duct			30 Gy
Duodenum	<5 cc <10 cc	11.2 Gy 9 Gy	17 Gy
Liver	700 cc	11 Gy
Renal cortex (right & left)	200 cc	9.5 Gy
Jejunum/ileum	<30 cc	12.5 Gy	22 Gy
Colon	<20 cc	18 Gy	29.2 Gy
Rectum	<3.5 cc <20 cc	39 Gy 22 Gy	44.2 Gy
Ureter			35 Gy
Bladder wall	<15 cc	12 Gy	25 Gy
Penile bulb	<3 cc	16 Gy
Femoral heads	<10 cc	15 Gy
Renal hilum/vascular trunk	15 cc	14 Gy

Table 2: Volume-dose constraints and the maximum point doses (volume <0.035cc) for various issues/organs for a 3-fraction SRT/SBRT treatment. Circumferential irradiation should be avoided for tube-like organs such as esophagus, bronchus, duodenum, jejunum/ileum, colon and rectum.              

Tissue/Organ	Volume	Volume Max Dose	Max Point Dose
Optic pathway	<0.2 cc	15.3 Gy	17.4 Gy
Cochlea			14.4 Gy
Brainstem (not medulla)	<0.5 cc	15.9 Gy	23.1 Gy
Spinal cord and medulla (10cm above and below treatment target)	<0.35 cc <1.2 cc	15.9 Gy 13 Gy	22.5 Gy
Spinal cord subvolume (5-6mm above and below treatment target)	<10%	18 Gy	22.5 Gy
Cauda equina	<5 cc	21.9 Gy	25.5 Gy
Sacral plexus	<5 cc	22.5 Gy	24 Gy
Esophagus	<5 cc	17.7 Gy	25.2 Gy
Brachial plexus	<3 cc	22 Gy	26  Gy
Heart/pericardium	<15 cc	24 Gy	30 Gy
Great vessels	<10 cc	39 Gy	45 Gy
Trachea and large bronchus	<5 cc	25.8 Gy	30 Gy
Bronchus- smaller airways	<0.5 cc	18.9 Gy	23.1 Gy
Lung (right & left)	1500 cc	10.5 Gy
Lung (right & left)	1000 cc	11.4 Gy	V11Gy<37%
Rib	<5 cc	40 Gy	50 Gy
Skin	<10 cc	31 Gy	33 Gy
Stomach	<5 cc	22.5 Gy	30 Gy
Bile duct			36 Gy
Duodenum	<5 cc <10 cc	15.6 Gy 12.9 Gy	22.2 Gy
Liver	700 cc	17.1 Gy
Renal cortex (right & left)	200 cc	15 Gy
Jejunum/ileum	<30 cc	17.4 Gy	27 Gy
Colon	<20 cc	24 Gy	34.5 Gy
Rectum	<3.5 cc <20 cc	45 Gy 27.5 Gy	49.5 Gy
Ureter			40 Gy
Bladder wall	<15 cc	17 Gy	33 Gy
Penile bulb	<3 cc	25 Gy
Femoral heads	<10 cc	24 Gy
Renal hilum/vascular trunk	15 cc	19.5 Gy

Table 3: Volume-dose constraints and the maximum point doses (volume <0.035cc) for various issues/organs for a 4-fraction SRT/SBRT treatment. Circumferential irradiation should be avoided for tube-like organs such as esophagus, bronchus, duodenum, jejunum/ileum, colon and rectum.                             

Tissue/Organ	Volume	Volume Max Dose	Max Point Dose
Optic pathway	<0.2 cc	19.2 Gy	21.2 Gy
Cochlea			18 Gy
Brainstem (not medulla)	<0.5 cc	20.8 Gy	27.2 Gy
Spinal cord and medulla (10cm above and below treatment target)	<0.35 cc <1.2 cc	18 Gy 14.6 Gy	25.6 Gy
Spinal cord subvolume (5-6mm above and below treatment target)	<10%	18 Gy	25.6 Gy
Cauda equina	<5 cc	26 Gy	28.8 Gy
Sacral plexus	<5 cc	26 Gy	28 Gy
Esophagus	<5 cc	18.8 Gy	30 Gy
Brachial plexus	<3 cc	24.8 Gy	29.6 Gy
Heart/pericardium	<15 cc	28 Gy	34 Gy
Great vessels	<10 cc	43 Gy	49 Gy
Trachea and large bronchus	<5 cc	28.8 Gy	34.8 Gy
Bronchus- smaller airways	<0.5 cc	20 Gy	28 Gy
Lung (right & left)	1500 cc	11.6 Gy
Lung (right & left)	1000 cc	12.4 Gy	V13Gy<37%
Rib	<5 cc	43 Gy	54 Gy
Skin	<10 cc	33.6 Gy	36 Gy
Stomach	<5 cc	25 Gy	33.2 Gy
Bile duct			38.4 Gy
Duodenum	<5 cc <10 cc	17.2 Gy 14 Gy	24.4 Gy
Liver	700 cc	19.2 Gy
Renal cortex (right & left)	200 cc	17 Gy
Jejunum/ileum	<30 cc	18.8 Gy	30 Gy
Colon	<20 cc	26 Gy	37.2 Gy
Rectum	<3.5 cc <20 cc	47.2 Gy 30 Gy	52.4 Gy
Ureter			43 Gy
Bladder wall	<15 cc	18.5 Gy	35.6 Gy
Penile bulb	<3 cc	27 Gy
Femoral heads	<10 cc	27 Gy
Renal hilum/vascular trunk	15 cc	21.5 Gy

Table 4: Volume-dose constraints and the maximum point doses (volume <0.035cc) for various issues/organs for a 5-fraction SRT/SBRT treatment. Circumferential irradiation should be avoided for tube-like organs such as esophagus, bronchus, duodenum, jejunum/ileum, colon and rectum.

Tissue/Organ	Volume	Volume Max Dose	Max Point Dose
Optic pathway	<0.2 cc	23 Gy	25 Gy
Cochlea			22 Gy
Brainstem (not medulla)	<0.5 cc	23 Gy	31 Gy
Spinal cord and medulla (10cm above and below treatment target)	<0.35 cc <1.2 cc	22 Gy 15.6 Gy	28 Gy
Spinal cord subvolume (5-6mm above and below treatment target)	<10%	22 Gy	28 Gy
Cauda equina	<5 cc	30 Gy	31.5 Gy
Sacral plexus	<5 cc	30 Gy	32 Gy
Esophagus	<5 cc	19.5 Gy	35 Gy
Brachial plexus	<3 cc	27 Gy	32.5 Gy
Heart/pericardium	<15 cc	32 Gy	38 Gy
Great vessels	<10 cc	47 Gy	53 Gy
Trachea and large bronchus	<5 cc	32 Gy	40 Gy
Bronchus- smaller airways	<0.5 cc	21 Gy	33 Gy
Lung (right & left)	1500 cc	12.5 Gy
Lung (right & left)	1000 cc	13.5 Gy	V13.5Gy<37%
Rib	<5 cc	45 Gy	57 Gy
Skin	<10 cc	36.5 Gy	38.5 Gy
Stomach	<5cc	26.5 Gy	35 Gy
Bile duct			41 Gy
Duodenum	<5 cc <10 cc	18.5 Gy 14.5 Gy	26 Gy
Liver	700 cc	21 Gy
Renal cortex (right & left)	200 cc	18 Gy
Jejunum/ileum	<30 cc	20 Gy	32 Gy
Colon	<20 cc	28.5 Gy	40 Gy
Rectum	<3.5 cc <20 cc	50 Gy 32.5 Gy	55 Gy
Ureter			45 Gy
Bladder wall	<15 cc	20 Gy	38 Gy
Penile bulb	<3 cc	30 Gy
Femoral heads	<10 cc	30 Gy
Renal hilum/vascular trunk	15 cc	23 Gy

Table 5: Volume-dose constraints and the maximum point doses (volume <0.035cc) for various issues/organs for an 8-fraction SRT/SBRT treatment. Circumferential irradiation should be avoided for tube-like organs such as esophagus, bronchus, duodenum, jejunum/ileum, colon and rectum.                                                                  

Tissue/Organ	Volume	Volume Max Dose	Max Point Dose
Optic pathway	<0.2 cc	27.2 Gy	29.6 Gy
Cochlea			26.4 Gy
Brainstem (not medulla)	<0.5 cc	27.2 Gy	37.6 Gy
Spinal cord and medulla (10cm above and below treatment target)	<0.35 cc <1.2 cc	26.4 Gy 18.2 Gy	33.6 Gy
Spinal cord subvolume (5-6mm above and below treatment target)	<10%	26.4 Gy	33.6 Gy
Cauda equina	<5 cc	36 Gy	38.4  Gy
Sacral plexus	<5 cc	36 Gy	38.4  Gy
Esophagus	<5 cc	21.6 Gy	38.4 Gy
Brachial plexus	<3 cc	32.8 Gy	39.2 Gy
Heart/pericardium	<15 cc	34.4 Gy	38.4 Gy
Great vessels	<10 cc	55.2 Gy	38.4 Gy
Trachea and large bronchus	<5 cc	38.4 Gy	48.8 Gy
Bronchus- smaller airways	<0.5 cc	22.4 Gy	36 Gy
Lung (right & left)	1500 cc	13.6 Gy
Lung (right & left)	1000 cc	15.2 Gy	V15Gy<37%
Rib	<5 cc	50 Gy	63 Gy
Skin	<10 cc	43.2 Gy	45.6 Gy
Stomach	<5 cc	31.2 Gy	42 Gy
Bile duct			48 Gy
Duodenum	<5 cc <10 cc	21 Gy 16 Gy	30.4 Gy
Liver	700 cc	24 Gy
Renal cortex (right & left)	200 cc	21 Gy
Jejunum/ileum	<30 cc	23.2 Gy	37 Gy
Colon	<20 cc	33 Gy	48 Gy
Rectum	<3.5 cc <20 cc	58.4 Gy 37.5 Gy	63.2 Gy
Ureter			53 Gy
Bladder wall	<15 cc	22.4 Gy	44.8 Gy
Penile bulb	<3 cc	35
Femoral heads	<10 cc	35 Gy
Renal hilum/vascular trunk	15 cc	28 Gy

After plan optimization, the dose distribution can be renormalized so that the target prescription dose and the total fraction number can be determined based on the maximum critical organ/structure volume-dose and the maximum point dose values achievable/acceptable for the plan under consideration. It should be noted that the values in Tables 1-5 should be used with caution since most of them were extrapolated/converted from the dose tolerances for conventional-dose/fractionation treatments using the linear-quadratic model [38,40]. On the other hand, one can derive the volume-dose constraints and the maximum point dose limits using the linear-quadratic model for fraction numbers not included in Tables 1 to 5.

Dosimetry Measurement

SRS and SBRT utilize small photon fields to achieve the desired, highly modulated and conformal dose distribution. Measurement of small photon beams for SRS and SBRT TPS commissioning and plan validation is complicated due to conditions of charged particle disequilibrium, detector volume-averaging effects, detector-interface artifacts, detector perturbation effects, and detector position-orientation effects [9]. For small field dosimetry, the AAPM Task Group 101 recommends the use of an appropriate dosimeter with a spatial resolution of approximately 1 mm or better (stereotactic detectors). Even with stereotactic detectors and careful measurement setup, large (> 10%) measurement discrepancies have been reported for cone factors of very small (<10mm) photon fields [41,42].

AAPM Task Group 101 discussed the issue of small field dosimetry in great detail and provided useful recommendations for beam commissioning and plan validation. For SRS and SBRT beam commissioning, the maximum dimension of the active detector volume should be less than half the full width at half maximum (FWHM) of the smallest photon field in order to determine the central axis depth dose, tissue-phantom ratio, output factor and scatter factor. For the lateral dose profile or off-axis ratio measurement, one can unfold the chamber size effect from measured small beam profiles by deconvolving the detector-response artifact from each point in the profiles. The detector volume effect only becomes significant when the maximum dimension of the active detector volume is comparable to the half size of the small photon fields.

Because of the small dimensions and rapid fall-offs of SRS and SBRT dose distribution, only those adequate detectors should be used, as recommended by the joint IAEA-AAPM report [43]. For SRS and SBRT dose measurement, large errors are often associated with small setup errors or measuring point misplacement. Measurements for MLC-shaped fields also show more geometric and dosimetric uncertainties than those for fields collimated by circular cones. This is mainly due to the complex MLC leaf geometry (tongue and groove and leaf end) and mechanical uncertainty. For small MLC fields, the leaf-edge effect depends mainly on the field size and type of MLC and is not related to the depth [44]. For more detailed discussions on small field dosimetry, please refer to the recently published report “An IAEA–AAPM International Code of Practice for Reference and Relative Dose Determination. Technical Report Series No. 483” [43].

REFERENCES

1. Leksell L. (1951). The stereotaxic method and radiosurgery of the brain. Acta Chir Scand. 102 (4): 316-319.
2. Gildenberg PL. (1988). Stereotactic Surgery: Present and Past, Stereotactic Neurosurgery, M. Peter Heilbrun Eds. Lippincott Williams and Wilkins, PA, USA.
3. Wu A, Lindner G, Maitz AH, Kalend AM.  (1990). Physics of Gamma Knife approach on convergent beams in stereotactic radiosurgery. Int J Radiat Oncol Biol Phys. 18(4): 941-949.
4. Xia T, Li H, Li P, Sun Q, et al. (2006). Promising clinical outcome of stereotactic body radiation therapy for patients with inoperable Stage I/II non–small-cell lung cancer. Int J Radiat Oncol Biol Phys. 66(1): 117–125.
5. Fareed MM, Eldib AA, Weiss SE, Hayes SB, et al. (2018). A treatment planning comparison between a novel rotating gamma system and robotic linear accelerator based intracranial stereotactic radiosurgery/radiotherapy. Phys Med Biol. 63(3): 1361-6560.
6. Winston KR, Lutz W. (1988). Linear accelerator as a neurosurgical tool for stereotactic radiosurgery. Neurosurgery. 22(3): 454-464.
7. Ma CM, ElDib A, Chibani O, Mora G, Li JS and Chen L. (2018). An advanced image-guided rotating Gamma ray system for intra- and extra-cranial SRS/SRT, MT19 - Radiation Oncology Physics and Systems. World Congress on Medical Physics and Biomedical Engineering, Prague, Czech Republic.
8. Ma CM and Lomax T, Ed., Proton and carbon ion therapy (Taylor & Francis, New York, 2012).
9. Benedict SH, Yenice KM, Followill D, Galvin JM, et al.  (2010). Stereotactic body radiation therapy: The report of AAPM Task Group 101.  Med Phys. 37(8): 4078-4101.
10. ICRU Report 62. (1999) Prescribing, Recording and Reporting Photon Beam Therapy (Supplement to ICRU Report 50) (International Commission on Radiation Units and Measurements, Bethesda, MD) [Internet].
11. Wang L and Ma CM. (2012). Dose Calculation Algorithms. In Encyclopedia of Radiation Oncology, Springer, Berlin, Germany.
12. Clarkson JR. (1941). A note on depth doses in fields of irregular shape. Br J Radiol. 14: 265-268.
13. Ahnesjo A. (1989). Collapsed cone convolution of radiant energy for photon dose calculation in heterogeneous media. Med Phys. 16(4): 577-592.
14. Ma CM, Chetty IJ, Deng J, Faddegon B, et al. (2019). Beam modeling and beam model commissioning for MC dose calculation based radiation therapy treatment planning: Report of AAPM Task Group 157. Med Phys. PMID: 31679157.
15. Chetty I, Curran B, Cygler J, DeMarco J, et al. (2007).  Report of The AAPM Task Group No. 105: Issues associated with clinical implementation of Monte Carlo-based photon and electron external beam treatment planning. Med Phys. 34(12): 4818-4853.
16. Heath E, Seuntjens J, Sheikh-Bagheri D. (2004). Dosimetric evaluation of the clinical implementation of the first commercial IMRT Monte Carlo treatment planning system at 6 MV. Med Phys. 31(10): 2771-2779.
17. Ma CM, Li JS, Deng J and Fan J. (2008). Implementation of Monte Carlo Dose Calculation for CyberKnife treatment planning. Journal of Physics: Conference Series 102: 012016 (1-10).
18. Papanikolaou N, Battista JJ, Boyer AL, Kappas C, et al. (2004) .Tissue inhomogeneity corrections for megavoltage photon beams, in AAPM Report No. 85. Medical Physics. Madison, WI, USA, 1-135.
19. Sikora M, Dohm D, Alber M. (2007). A virtual photon beam model of an Elekta linear accelerator with integrated mini MLC for MC based IMRT dose calculation.  Phys Med Biol. 52: 4449-4463.
20. Dempsey JF, Romeijn HE, Li JG, Low DA, et al. (2005). A Fourier analysis of the dose grid resolution required for accurate IMRT fluence map optimization.  Med Phys. 32(2): 380-388.
21. Bedford JL, Childs PJ, Nordmark Hansen V,  Mosleh-Shirazi MA, et al. (2003). Commissioning and quality assurance of the Pinnacle radiotherapy treatment planning system for external beam photons. Br J Radiol. 76(903): 163-176.
22. Chung H, Jin H, Palta J, Suh TS, et al. (2006). Dose variations with varying calculation grid size in head and neck IMRT.  Phys Med Biol. 51(19): 4841-4856.
23. Buyyounouski MK, Balter P, Lewis B, D'Ambrosio DJ, et al. (2010). Stereotactic Body Radiotherapy for Early-Stage Non-Small-Cell Lung Cancer: Report of the ASTRO Emerging Technology Committee. Int J Radiat Oncol Biol Phys. 78: 3-10.
24. Ma CM, Li CH, ElDib A, Chibani O, et al. (2015). A Dosimetric Study of an Advanced SRS/SRT System for Intra/Extracranial Tumors. Int J Radiat Oncol Biol Phys. 93: E564.
25. Ding M, Newman F, Chen C, Stuhr K, et al. (2009). Dosimetric 434comparison  between  3DCRT  and  IMRT  using  different  multileaf  collimators  in the treatment of brain tumors. Med Dosim. 34(1): 1-8.
26. Blomgren H, Lax I, Goranson H, Kraepelien T, et al. (1998). Radiosurgery for tumors in the body: clinical experience using a new method. J Radiosurg. 1(1): 63-74.
27. Rusthoven KE, Kavanagh BD, Cardenes H, Stieber VW, et al. (2009). Multi-institutional phase I/II trial of stereotactic body radiation therapy for liver metastases. J Clin Oncol. 27(10): 1572-1578.
28. Rule W, Timmerman R, Tong L, Abdulrahman R, et al. (2011). Phase I dose-escalation study of stereotactic body radiotherapy in patients with hepatic metastases. Ann Surg Oncol. 18(4): 1081-1087.
29. Chang DT, Swaminath A, Kozak M, Weintraub J, e tal. (2011). Stereotactic body radiotherapy for colorectal liver metastases: a pooled analysis. Cancer. 117(17): 4060-4069.
30. Berber B, Ibarra R, Snyder L, Yao M, Fabien J, et al. (2013). Multicentre results of stereotactic body radiotherapy for secondary liver tumours. HPB (Oxford). 15(11): 851-857.
31. Koong AC, Christofferson E, Le QT, Goodman KA, et al. (2005). Phase II study to assess the efficacy of conventionally fractionated radiotherapy followed by a stereotactic radiosurgery boost in patients with locally advanced pancreatic cancer. Int J Radiat Oncol Biol Phys. 63(2): 320-323.
32. Schellenberg D, Goodman K A, Lee F, Chang S, et al. (2008). Gemcitabine chemotherapy and single-fraction stereotactic body radiotherapy for locally advanced pancreatic cancer. Int J Radiat Oncol Biol Phys. 72(3): 678-686.
33. Hoyer M, Roed H, Sengelov L,Traberg A, et al. (2005). Phase-II study on stereotactic radiotherapy of locally advanced pancreatic carcinoma. Radiother Oncol. 76(1): 48-53.
34. Mahadevan A, Jain S, Goldstein M, Miksad R, et al. (2010). Stereotactic body radiotherapy and gemcitabine for locally advanced pancreatic cancer. Int J Radiat Oncol Biol Phys. 78(3):735-742.
35. Polistina F, Costantin G, Casamassima F, Francescon P, et al. (2010). Unresectable locally advanced pancreatic cancer: a multimodal treatment using neoadjuvant chemoradiotherapy (gemcitabine plus stereotactic radiosurgery) and subsequent surgical exploration. Ann Surg Oncol. 17(8): 2092-2101.
36. Gurka MK, Collins SP, Slack R, Tse G, et al. (2013). Stereotactic body radiation therapy with concurrent full-dose gemcitabine for locally advanced pancreatic cancer: a pilot trial demonstrating safety. Radiat Oncol. 8:44.
37. Herman JM, Chang DT, Goodman KA, Dholakia AS, et al. (2015). Phase 2 multi-institutional trial evaluating gemcitabine and stereotactic body radiotherapy for patients with locally advanced unresectable pancreatic adenocarcinoma. Cancer. 121(7): 1128-1137.
38. Timmerman RD. (2008). An overview of hypofractionation and introduction to this issue of seminars in radiation oncology. Semin Radiat Oncol. 18(4): 215-222.
39. Emami B. (2013). Tolerance of Normal Tissue to Therapeutic Radiation. Rep Radiother Oncol. 1(1): 123-127.
40. Fowler JF. (1989) .The linear-quadratic formula and progress in fractionated radiotherapy. Br J Radiol. 62: 679-694.
41. Cheung JY, Yu KN, Ho RT, Yu CP. (1999). Monte Carlo calculatedoutput factors of a Leksell Gamma Knife unit. Phys Med Biol. 44(12): N247-N249.
42. De Vlamynck K, Palmans KH, Verhaegen F, De Wagter C, et al. (1999). Dose measurements compared with Monte Carlo simu-lations of narrow 6 MV multileaf collimator shaped photon beams. Med Phys. 26(9): 1874-1882.
43. Palmans H, Andreo P, Huq MS, Seuntjens J, et al. (2017). Dosimetry of Small Static Fields used in External Beam Radiotherapy: An IAEA–AAPM International Code of Practice for Reference and Relative Dose Determination. Technical Report Series No. 483. Vienna: International Atomic Energy Agency.
44. Li S, Rashid A, He S, Djajaputra. (2004). A new approach in dosemeasurement and error analysis for narrow photon beams beamlets shaped by different multileaf collimators using a small detector. Med Phys. 31(7):  2020–2032.