Fraction-Modulated Dose Optimization for Advanced Radiation Therapy

Department of Radiation Oncology, Fox Chase Cancer Center, Philadelphia, PA 19111, USA

*Corresponding author: CM Charlie Ma, Ph.D., Radiation Oncology Department, Fox Chase Cancer Center, 333 Cottman Avenue, Philadelphia, PA 19111, USA; Tel: (215) 728-2996; Fax: (215) 728-4789; Email: [email protected]

Received Date: March 3, 2024

Publication Date: March 17, 2024

Citation: Ma CMC, et al. (2024). Fraction-Modulated Dose Optimization for Advanced Radiation Therapy. Mathews J Cancer Sci. 9(1):47.

Copyright: Ma CMC, et al. © (2024)

ABSTRACT

The recent growth in technology of radiation treatment machines has resulted in advanced radiation therapy treatment techniques that deliver conformal dose distributions to cover treatment targets while sparing nearby critical structures. This has further facilitated clinical trials on dose escalation and fractionation to explore advanced treatment strategies for further improvement in tumor control and normal tissue toxicities. Radiobiological dose conversion plays an important role in conventionally fractionated radiation therapy (CFRT) that employs daily 2 Gy/fractions and stereotactic body radiotherapy (SBRT) that employs ablative doses (8-30Gy/fraction). This work investigates the radiobiological dose characteristics of CFRT and SBRT and the potential application of fraction-modulated dose optimization (FMDO) for advanced treatment planning. Physical dose distributions were converted to the biologically equivalent dose in 2-Gy fractions (EQD2) for tumors with an α/β ratio of 10 Gy and for normal tissues with an α/β ratio of 3 Gy. The Prowess Panther TPS was used for the EQD2 conversion and for FMDO-based plan optimization, in which the dose, fractionation and tissue radio-sensitivity are built in the planning objectives. The results showed that EQD2 in normal tissues immediately outside the target volume was much greater than EQD2 in the target, especially with fewer treatment fractions. The difference in EQD2 between the target and normal tissues decreased rapidly with the increasing distance from the target, and it reversed roughly outside V_50%Dp, the volume receiving 50% of the prescription dose. This is an important finding as the reversed EQD2 difference is the basis for SBRT parameters such as R50% and for FMDO-based treatment planning, which is beneficial to complex cases with multiple targets and overlapping target-OAR geometries. Realistic clinical cases demonstrated that doses to critical structures outside V_{50% Dp} could be reduced significantly (up to 50%) with SBRT compared with CFRT using the FMDO technique.

Keywords: Conventional fractionation radiation therapy (CFRT), stereotactic body radiation therapy (SBRT), radiobiology, EQD2, treatment planning, fraction-modulated dose optimization (FMDO)

INTRODUCTION

The recent development of radiotherapy (RT) equipment and treatment techniques has led to a paradigm shift from conventionally fractionated radiation therapy (CFRT) that typically employs 2 Gy daily doses to stereotactic body radiation therapy (SBRT) that employs ablative large doses, e.g., 8 - 30Gy/fraction (Kavanagh and Timmerman 2005, Posky et al 2012) [1,2]. Early clinical outcomes for primary and metastatic lung and liver malignancies have demonstrated the efficacy of SBRT with superior local control and acceptable normal tissue toxicities (Herfarth et al 2001, Timmerman et al 2003, 2006, Schefter et al 2005, Hara et al 2006, Chang et al 2015) [3-8]. Radiobiological dose conversion plays an important role in the design of SBRT plans to achieve desired tumor control and to reduce normal tissue toxicities, and for outcome analyses between CFRT and SBRT. For example, to achieve the same or better tumor control for SBRT, the biologically equivalent dose in 2-Gy fractions (EQD2) for the target volume (assuming an a/b ratio of 10 Gy) must be equal to or greater than the prescription dose for CFRT. To keep normal issue toxicities below acceptable levels, the tolerance doses for various organs and normal structures in EQD2 are converted with corresponding a/b ratios (e.g., 3 Gy for most late-responding tissues) based on previous knowledge and experience with CFRT (Fowler 1989, Timmerman 2008, Ma 2019) [9-11].

It is well known that for the same physical dose distributions, the EQD2 values converted for late-responding tissues such as most normal tissues with a low α/β ratio of ~3 Gy can be much different than those for early responding tissues and most tumors with a high α/β ratio of ~10 Gy between SBRT and CFRT (Hall 1978, Fowler 2010) [12,13]. In general, early responding tissue proliferates quickly while late responding tissues tend to be slower growing with a longer cell cycle. For example, the SBRT target dose prescription of 50 Gy in 5 fractions results in an EQD2 value of 83.3 Gy for the tumor (assuming α/β = 10 Gy), which is higher than the typical CFRT prescription dose of 60 – 80 Gy, and 130 Gy for normal tissues (assuming α/β = 3 Gy), which is much higher than the normal tissue doses received in CFRT, typically < 80 Gy. Because of such a difference in radiobiological response (i.e., in terms of EQD2) between tumors and normal tissues, it is expected that in SBRT a layer of normal tissues surrounding the target volume would also get damaged if the prescription dose to the target is ablative. This high-EQD2 volume of normal tissues surrounding the target (or the intermediate dose spill) increases rapidly with the increasing target size and decreasing dose gradient outside the target. Therefore, in order to minimize normal tissue toxicities, it is important to keep the target volume small and to design the SBRT dose distribution with a sharper dose falloff outside the target volume.

According to RTOG 0915 (Videtic et al 2015) [14], intermediate dose spill in SBRT is quantified by R50%, which is the ratio of the 50% prescription isodose volume to the planning target volume (PTV). A greater R50% also indicates a larger volume of normal tissues that receive doses equal to or greater than 50% of the prescription dose to the target. R50% is conceptually similar to the dose gradient index (DGI), which is a widely used dosimetric parameter for stereotactic radiosurgery (SRS) treatment planning to quantify the dose falloff outside the target (Wagner et al 2003) [15]. DGI is calculated based on the difference of the effective radius of the 50% prescription isodose volume, R_eff,50%, and the effective radius of the 100% prescription isodose volume, R_eff,100%. The effective radius of a volume is the radius of a sphere of equal volume V (i.e., V = ). Clearly, DGI is also concerned about nearby normal tissues that receive doses equal to or greater than 50% of the prescription dose to the target. However, no details have been discussed as to why 50% of the prescription dose to the target was selected as a dose threshold to evaluate dose falloff or intermediate dose spill for SRS/SBRT plan quality analysis.

In this work, we convert the physical doses from CFRT in 2 Gy per fraction to EQD2 for SBRT (in 1 -5 fractions) using the linear-quadratic (LQ) model (Fowler 1989) [9] to investigate the EQD2 characteristics of early responding-tissues and late-responding tissues and their impact on the target dose prescription and normal tissue constraints for SBRT treatment planning. The differential radiobiological responses (i.e., EQD2) between early- and late-responding tissues are investigated including the reversal of EQD2 at about 50% of the prescription dose in the nearby normal tissues, which not only serve as the dosimetric basis for the plan quality parameters such as DGI and R50% but also provide possibilities for fraction-modulated dose optimization (FMDO) for SBRT treatment planning. Simple dose distributions and realistic patient plans are used to demonstrate the EQD2 characteristics and FMDO benefits.

MATERIALS AND METHODS

The LQ model

The LQ model (Fowler 1989) [9] approximates clonogenic cell survival fraction S as:

S =                                                                                                                                         (1)

where d is the absorbed dose in Gy (J/kg), and a and b are model parameters that determine the relative contributions from the linear and quadratic components of the cell survival curve, respectively. Parameter a is the slope of the cell survival curve at the limit d → 0, and the a/b ratio is the dose at which the linear and quadratic components of cell kill are equal.

The EQD2 formula

In CFRT, the prescription dose to the target is typically given in 2 Gy per fraction. Therefore, most clinical outcome data for local tumor control and normal tissue toxicities are based on 2 Gy/fraction dose schemes. For SBRT with a different fractional dose d, it would be useful to know the total equivalent dose of the particular dose fractionation at 2 Gy fractions, i.e., EQD2 (Fowler 2010) [13]. Based on the LQ formula of Eq. (1), EQD2 can be calculated as

                                                                             (2)

where d is the physical dose per fraction, n is the number of fractions for the treatment scheme and D = nd is the total physical dose for the entire treatment course. EQD2 has been used in designing hyper- or hypofractionated, especially SBRT clinical trials to set up dose limits for treatment targets and organs at risk (OAR) and in outcome analyses.

Dose Conversion for the Target and Normal Tissues

Equation (2) can be used to convert the total physical dose D from an SBRT treatment plan to EQD2 in order to compare with CFRT treatment plans. In SBRT planning, on the other hand, it is often necessary to determine the physical fractional dose d for a given number of treatment fractions n in order to achieve the same EQD2 (i.e., for the same tumor control). This can be achieved by scaling the same physical dose distribution of a given SBRT by changing the monitor units accordingly. Thus, based on Eq. (2) we have

nd² + nd a/b – (2 + a/b) EQD2 = 0                                                     (3)

Thus, we can calculate d based on a/b, n and EQD2, i.e.,

d =  -                                       (4)

For example, assuming a/b = 10 Gy for the target, we can calculate the SRS/SBRT physical dose per fraction for the target from

d =  - 5                                                                    (5)

Another useful dosimetric quantity for SBRT is the ratio of the EQD2_n for normal tissues to EQD2_t for the target when both receive the same physical dose, which can be used to estimate the potential increase of normal tissue toxicities. Based on Eq. (2) we have

                                                                            (6)

Assuming a/b = 10 Gy for the target and 3 Gy for normal tissues, we can calculate this EQD2 ratio at the target boundary as

                                                                                     (7)

It is clear that for SBRT, a normal tissue with a smaller a/b than that of the target will always receive a higher EQD2 than that of the target when irradiated by a physical dose > 2 Gy, and it increases with the fractional dose d (and the decreasing number of treatment fractions according to Eq. 4).

The Prowess TPS

The Prowess Panther treatment planning system (version 5.60.4657, Prowess Inc., Concord, CA) was used in this work to generate SBRT treatment plans and to convert physical dose distributions to EQD2 distributions. The dose calculation was performed using the collapsed cone convolution (CCC) algorithm (Luong et al 2019) [16] and the plan optimization was based on the direct aperture optimization (DAO) algorithm (Shepard et al 2002) [17] for both intensity-modulated radiation therapy (IMRT) and volumetric-modulated arc therapy (VMAT). The target prescription dose per fraction was determined based on Eq. (4) and the EQD2 distribution was calculated using Eq. (2). The Panther TPS also has an option to optimize a treatment plan based on an existing dose distribution, which enables plan optimization with different dose fractionation. For example, one can optimize an SBRT plan, convert the dose distribution to EQD2, and then optimize a CFRT plan based on the existing EQD2 distribution to achieve a desired target coverage and normal tissue sparing for a combined SBRT/CFRT treatment plan.

RESULTS

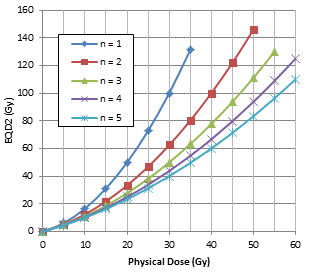
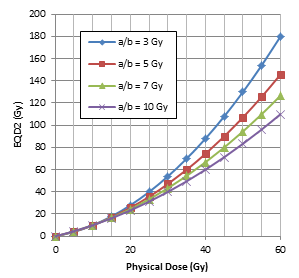
We have investigated the EQD2 characteristics as a function of the physical dose D and SBRT fractionation scheme. Figure 1(a) shows the EQD2 values converted from the physical dose D for SBRT with the number of fractions 1, 2, 3 , 4 and 5 using Eq. (2) assuming a/b = 10 Gy. Clearly, EQD2 increases with the physical dose D, but more rapidly with a decreasing number of fractions. Figure 1(b) shows the EQD2 values converted from physical dose D for SBRT in 5 fractions with an a/b ratio of 3, 5, 7 and 10 Gy. Again, EQD2 increases with the physical dose D, but more rapidly with decreasing a/b ratios. It is well understood that the dosimetric enhancement (i.e., the increase in EQD2) of SBRT is more significant with lower a/b ratios (e.g., prostate tumors and late-responding normal tissues) and fewer treatment fractions. It is therefore important to keep a rapid dose falloff outside the target to reduce normal tissue toxicities.

Table 1 shows the physical fractional dose d required to achieve an EQD2 value of 60, 80 and 100 Gy, respectively, for SBRT with 1 to 5 fractions assuming an a/b ratio of 10 Gy for the target according Eq. (5) and the EQD2 ratio of normal tissues to the target R_n,t assuming an a/b ratio of 3 Gy for normal tissues according to Eq. (7). Many tumors are prescribed with a total physical dose D = 60 Gy in 30 fractions for preventative, palliative or combinational treatments with other therapies, and prostate cancer is typically treated to 76-80 Gy in 38-40 fractions with CFRT. Only SBRT dose fractionation schemes have achieved ablative EQD2 values of 100 Gy and higher (e.g., for lung and liver cancers). SBRT is also used for local tumor control, palliation or pre-surgery tumor debulking (e.g., for prostate, pancreatic cancers) with EQD2 of 60-80 Gy (i.e., using physical fractional dose and fractionation schemes close to those listed in Table 1).

(a)                              (b)

Figure 1: EQD2 as a function of the physical dose D for the target assuming an a/b ratio of 10 Gy with 1, 2, 3, 4 and 5 fractions (a), and EQD2 as a function of D with 5 fractions assuming an a/b ratio of 3, 5, 7 and 10 Gy (b) calculated according to Eq. (2).

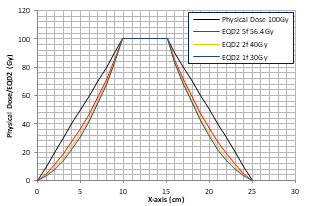
Since the EQD2 increase with the physical dose D is not linear the difference between EQD2 and the physical dose D increases rapidly at higher doses (Figure 1). This has an interesting effect on the penumbral EQD2 distribution of SBRT with few treatment fractions. Figure 2 shows a schematic physical dose distribution with the target (between 10 cm - 15 cm on the x-axis) receiving D = 100 Gy and linearly decreasing penumbral doses from 100 Gy to 0 Gy on both sides from 10 cm to 0 cm and from 15 cm to 25 cm on the x-axis. The same physical dose distribution can be re-scaled for SBRT to deliver 100 Gy EQD2 to the target in fewer fractions. The total physical dose (i.e., D = nd) for SBRT to achieve 100 Gy EQD2 can be found in Table 1 (e.g., D = 30 Gy for n = 1, 40 Gy for n = 2 and 56.4 Gy for n = 5). The EQD2 distributions converted based on the re-scaled physical doses for SBRT with 1, 2 and 5 fractions assuming a homogeneous tissue with an a/b ratio of 10 Gy are shown in Figure 2(a). The penumbral EQD2 for SBRT is much lower than the corresponding physical dose (or a sharper dose falloff with fewer fractions) due to the non-linear physical dose to EQD2 conversion effect, which is a reflection of the differential radiobiological response between CFRT and SBRT (i.e., the dose fractionation effect). The results for a uniform phantom with a/b = 3 Gy show similar trends with more rapid dose falloff (not shown).

Table 1:The physical fractional dose d for the target assuming an a/b ratio of 10 Gy to achieve an EQD2 value of 60, 80 and 100 Gy, respectively (Eq. 5), and the corresponding EQD2 ratio of normal tissues to the target R_n,t for the same physical fractional dose assuming an a/b ratio of 3 Gy for normal tissues (Eq. 7).

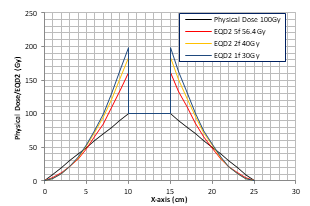
The situation becomes more complicated, however, if the target and surrounding tissues have different a/b ratios. Figure 2(b) shows the EQD2 distributions converted based on the re-scaled physical doses for SBRT with 1, 2 and 5 fractions assuming a/b = 10 Gy for the target and a/b = 3 Gy outside the target. A drastic increase of EQD2 is seen at the tissue-target boundary for SBRT with fewer fractions. For example, EQD2 for normal tissues is almost twice of that for a target with n = 1 (R_n,t = 1.98 in Table 1). It is interesting to note that the penumbral EQD2 decreases rapidly and the EQD2 ratio R_n,t is reversed at about 50% of the prescription dose (50%D_p). This means that the intermediate dose spill is likely to cause more normal tissue damage due to the differential radiobiological response with fewer fractions for SBRT than for CFRT. However, the normal tissues outside the 50%D_p isodose volume will always receive lower EQD2 in SBRT than the physical dose received in CFRT. This is an interesting observation, which can be utilized in SBRT planning to further reduce normal tissue toxicities based on fraction-modulated dose optimization (FMDO).

(a)                       (b)

Figure 2: The same physical dose distribution (black) rescaled to deliver D_p = 100 Gy EQD2 in the target region between 10 cm and 15 cm using 1, 2 and 5 fractions in a uniform tissue with a/b = 10 Gy (a), and the same physical dose distribution rescaled to deliver 100 Gy EQD2 using 1, 2 and 5 fractions with a/b =10 Gy in the target region and a/b = 3 Gy outside the target (b).

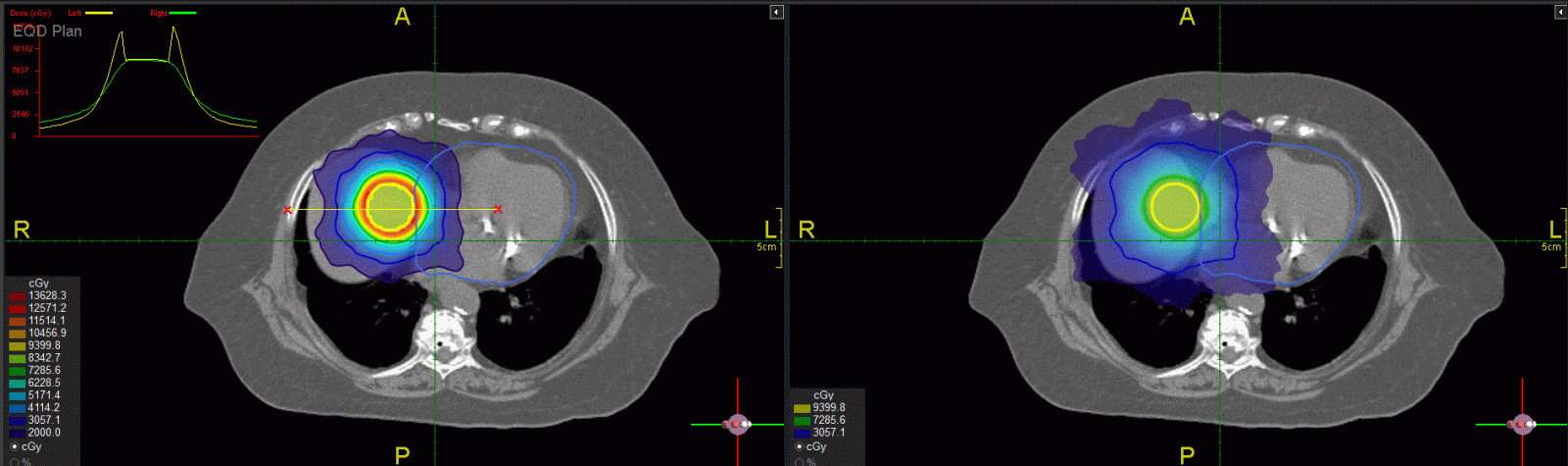
To demonstrate the idea of FMDO, we used the Prowess Panthers TPS to optimize physical dose distributions for the same target/critical structure geometry and then converted them to EQD2 to achieve the same target dose. Figure 3 shows a dummy target (contours in blue) in the liver adjacent to the heart (contours in light blue). The a/b ratio is 10 Gy for the target and 3 Gy for the liver and the heart. Since the target is next to the heart the intermediate dose spill for SBRT with 5 fractions (the left figure) is inside the heart with very high EQD2 values (yellow dose profile in the insert) immediately outside the target volume, which can potentially damage the heart as shown in the left figure. In contrast, the CFRT dose distribution on the right does not have such hot doses in the heart and presents a better dosimetric option although the low-dose (e.g., 20 Gy) region is larger than that of the SBRT plan on the left.

Figure 3: Comparison of dose distributions between SBRT in 5 fractions (left) and CFRT in 2 Gy fractions (right) planned using the Prowess Panthers TPS. The target is in the liver next to the heart (contours in light blue). The top left insert shows dose profiles along the yellow line between the red “x” signs: SBRT in 5 fractions (the yellow curve), CFRT in 2 Gy fractions (the green curve).

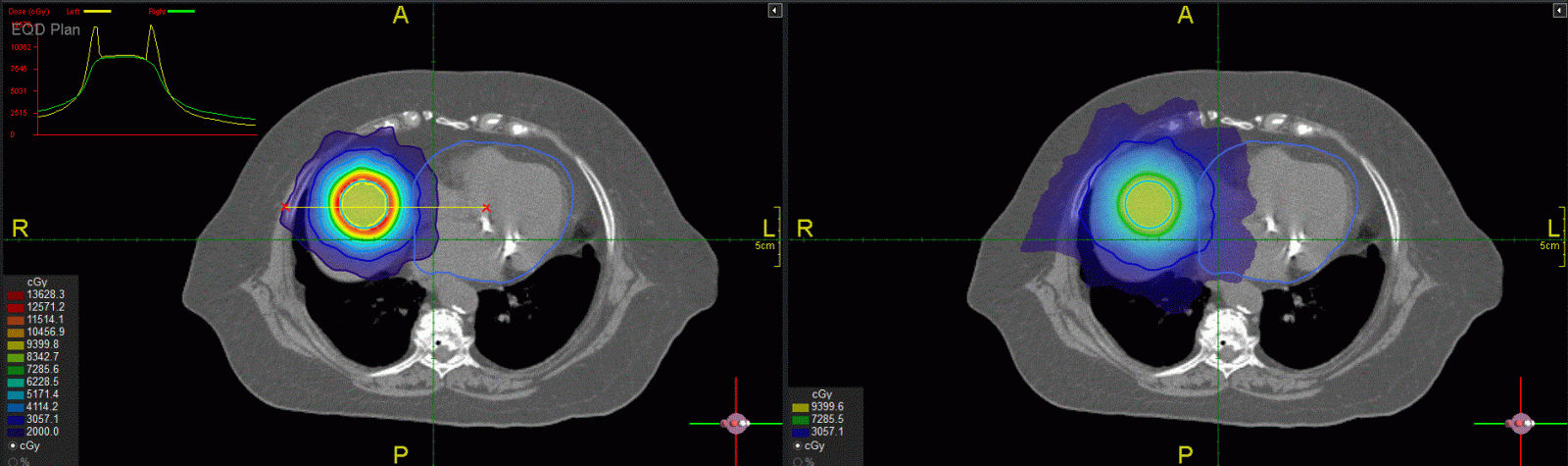
On the other hand, when a critical structure is away from the target, SBRT with fewer fractions may provide better dose distributions due to more favorable critical structure sparing. Figure 4 shows a dummy target (contours in blue) in the liver and the heart is outside the 50%D_p volume. The a/b ratio is 10 Gy for the target and 3 Gy for the liver and the heart. For SBRT with 5 fractions, the intermediate dose spill falls inside the liver (the left figure), which is a parallel organ that can tolerate much higher doses if only a small volume of subunits is involved. The EQD2 distribution for SBRT (the yellow dose profile in the insert) inside the heart is more favorable than the physical dose distribution for CFRT (the right figure), indicating that SBRT is clearly a better dosimetric option for this scenario. The same idea can be applied to clinical cases where serial organs may be better spared with SBRT using FMDO in treatment planning.

Figure 4: Comparison of dose distributions between SBRT in 5 fractions (left) and CFRT in 2 Gy fractions (right) planned using Prowess Panthers TPS. The target is in the liver outside the 50%D_p volume. The top left insert shows dose profiles along the yellow line between the red “x” signs: SBRT in 5 fractions (the yellow curve), CFRT in 2 Gy fractions (the green curve).

DISCUSSION

In this study, we have investigated the EQD2 characteristics for SBRT as a function of the physical dose, fractionation and radiobiological tissue response. The non-linear EQD2 conversion from the physical dose, especially with fewer treatment fractions and tissues with low a/b ratios, results in much faster EQD2 falloff outside the target if the target and surrounding tissues have similar a/b ratios (Figure 2a), which can be a significant advantage for SBRT treatments. For example, some tumors such as prostate and sarcoma have low a/b ratios, which are similar to those of late responding normal tissues and may justify the use of larger-than-standard dose fractionation in order to achieve significant cell-kill and better normal tissue sparing with the application of SBRT (Fowler 2001, Wang et al 2003, Cui et al 2022, Soyfer et al 2010, Elledge et al 2021, Gutkin et al 2023) [18-23]. Patients with sarcoma, prostate cancer or other cancers and poor performance status or severe co-morbidities, might benefit from attending a short course of SBRT and reduced normal tissue toxicities due to the sharper dose falloff with fewer treatment fractions.

A serendipitous finding is the reversal EQD2 ratio R_n,t for SBRT at a distance away from the target when surrounding normal tissues have lower a/b ratios than that of the target, which is true for most treatment geometries; the EQD2 value for SBRT is higher than the physical dose D for CFRT with D > 50%D_p and it becomes lower for D < 50%D_p assuming a/b= 3 Gy for normal tissues and a/b = 10 Gy for the target (e.g., Fig. 2b). This observation provides the dosimetric basis for the plan quality parameters, DGI and R50%, for SRS and SBRT. The EQD2 values are elevated in the surrounding normal tissues for D > 50%D_p (i.e., the intermediate dose spill) and, therefore, represent a higher risk for normal tissue damage. However, these parameters are more meaningful for dosimetry evaluation (e.g., to select a plan with a better dose distribution) or treatment optimization (e.g., to generate a plan with a sharper dose falloff) rather than for normal tissue toxicity prediction. The reason is that normal tissue toxicities are not usually observed at 50% D_p for D_p ≤ 80 Gy in CFRT or for non-ablative SBRT with EQD2 ≤ 80 Gy. Because of the large variation of the physical prescription dose and fractionation among clinical SBRT trials, 50%D_p has not correlated well with clinically observed normal tissue toxicities. The concept of “red shell” has been proposed to define and quantify normal tissue toxicities in SBRT (Yang et al 2010) [24], which is a dose zone surrounding the target that extends outward to a region of a threshold EQD2 for normal tissue damage. The outer surface of the red shell may be larger or smaller than the 50%D_p isodose surface depending on the value of the threshold EQD2, which varies with the physical dose, fractionation and a/b ratio of the tissue ranging from as high as 70 Gy to as low as 20 Gy for certain radiosensitive tissues. In parallel-structure tissues it can be higher for smaller volumes, e.g. EQD2 = 80 Gy in about 2 cc (Fowler et al 2010) [25].

A good application of the reversal EQD2 ratio R_n,t for SBRT is to design treatment plans based on fraction-modulated dose optimization (FMDO) to improve EQD2 distributions in critical structures for potential normal tissue toxicity reduction. When critical structures are located between the target and the 50%D_p isodose surface, CFRT in 2 Gy fractions or SBRT with more fractions will be more favorable than SBRT with fewer fractions especially if critical structures have lower a/b ratios (to reduce the red shell volume), as shown in Figure 3. Alternatively, when critical structures are located outside the 50%D_p isodose volume, their EQD2 distributions can be improved using SBRT with fewer fractions than SBRT with more fractions or CFRT, as shown in Figure 4. Furthermore, it is possible to optimize the treatment fraction number to achieve desirable EQD2 distributions in critical structures depending on their a/b ratios and threshold EQD2, which can be converted from the corresponding physical dose constraints (Timmerman 2008, Ma 2019) [10,11]. In particular, treatment plans including multiple targets and critical structures with complex geometry relationships can be optimized with FMDO to achieve better tumor control and normal tissue toxicities. FMDO can also play a role in treatment planning for re-irradiation scenarios where critical structure sparing takes a high priority. FMDO can be combined with other inverse planning strategies in which patient-specific radiosensitivities of tumors and normal tissues are directly factored into the optimization objective for advanced radiotherapy treatment (Polan et al 2022) [26]. Finally, it is necessary to point out that there are large uncertainties in the a/b values for most clinically relevant tissues (Fowler 1989, Wang et al 2003, Cui et al 2022, Ma 2023, Steel GG 2002) [9,19,20,27,28] and therefore FMDO should be used with caution in a clinical setting.

CONCLUSIONS

In this work, we have investigated the EQD2 characteristics as a function of physical dose, fractionation and tissue radiosensitivities. The results show that the non-linear conversion from physical dose to EQD2 can lead to sharper dose falloff for SBRT dose distributions with fewer fractions when the target and surrounding tissues have similar a/b ratios. CFRT or SBRT with more fractions are more suitable for treatment geometries where the target and surrounding tissues have very different radiosensitivities and there are critical structures inside the target volume or immediately adjacent to the target. The reversal of the EQD2 ratio of normal tissue to the target R_n,t on the penumbral dose region provides additional benefits for SBRT with fewer fractions to improve EQD2 distributions in surrounding normal tissues (to reduce the red shell volume). Fraction-modulated dose optimization has the potential to combine with other treatment planning techniques to further improve local tumor control and normal tissue toxicities for advanced radiation therapy.

ACKNOWLEDGMENTS

Technical support from Prowess Inc. is greatly appreciated for the implementation and application of EQD2 based treatment planning using the Panther TPS.

REFERENCES

1. Kavanagh BD, Timmerman RD. (2005). Stereotactic body radiation therapy, Lippincott Williams & Wilkins, Philadelphia, PA. 1-153.
2. Ponsky LE, Fuller DB, Meier RM, Ma CM (Eds). (2012). Robotic Radiosurgery Treating Prostate Cancer and Related Genitourinary Applications (Springer-Verlag, Berlin Heidelberg, 2012) Hardcover:245.
3. Herfarth KK, Debus J, Lohr F, Bahner ML, Rhein B, Fritz P, et al. (2001). Stereotactic single-dose radiation therapy of liver tumors: Results of a phase I/II trial. J Clin Oncol. 19:164–170.
4. Timmerman R, Papiez L, McGarry R, Likes L, DesRosiers C, Frost S, et al. (2003). Extracranial stereotactic radioablation: Results of a phase I study in medically inoperable stage I non-small cell lung cancer. Chest. 124:1946–1955.
5. Timmerman R, McGarry R, Yiannoutsos C, Papiez L, Tudor K, DeLuca J, et al. (2006). Excessive toxicity when treating central tumors in a phase II study of stereotactic body radiation therapy for medically inoperable early-stage lung cancer. J Clin Oncol. 24:4833–4839.
6. Schefter TE, Kavanagh BD, Timmerman RD, Cardenes HR, Baron A, Gaspar LE. (2005). A phase I trial of stereotactic body radiation therapy (SBRT) for liver metastases. Int J Radiat Oncol Biol Phys. 62:1371–1378.
7. Hara R, Itami J, Kondo T, Aruga T, Uno T, Sasano N, et al. (2006). Clinical outcomes of single fraction stereotactic radiation therapy of lung tumors. Cancer. 106:1347–1352.
8. Chang JY, Senan S, Paul MA, Mehran RJ, Louie AV, Balter P, et al. (2015). Stereotactic ablative radiotherapy versus lobectomy for operable stage I non-small-cell lung cancer: a pooled analysis of two randomised trials. Lancet Oncol. 16:630–637.
9. Fowler JF. (1989). The linear-quadratic formula and progress in fractionated radiotherapy. Br J Radiol. 62: 679–694.
10. Timmerman RD. (2008). An overview of hypofractionation and introduction to this issue of seminars in radiation oncology. Semin Radiat Oncol. 18(4):215-222.
11. Ma CM. (2019). Physics and Dosimetric Principles of SRS and SBRT, Mathews J Cancer Sci. 4(2):22.
12. Hall EJ, Curves C-S. (1978). Radiobiology For the Radiologist. New York: Harper & Row: 31–62.
13. Fowler JF. (2010). 21 years of biologically effective dose. Br J Radiol. 83(991):554-568.
14. Videtic GM, Paulus R, Singh AK, Chang JY, Parker W, Olivier KR, et al. (2015). A randomized phase 2 study comparing 2 stereotactic body radiation therapy schedules for medically inoperable patients with stage I peripheral non-small cell lung cancer: NRG Oncology RTOG 0915 (NCCTG N0927). Int J Radiat Oncol Biol Phys. 93:757–764.
15. Wagner TH, Bova FJ, Friedman WA, Buatti JM, Bouchet LG, Meeks SL. (2003). A simple and reliable index for scoring rival stereotactic radiosurgery plans. Int J Radiat Oncol Biol Phys. 57: 1141-1149.
16. Yang J, Fowler JF, Lamond JP, Lanciano R, Feng J, Brady LW. (2010). Red shell: defining a high-risk zone of normal tissue damage in stereotactic body radiation therapy. Int J Radiat Oncol Biol Phys. 77(3):903-909.
17. Luong O, Tai DT, Loan TTH, Minh TH, Minh TV, Chow JCL, et al. (2019). Dosimetric evaluation of lung treatment plans produced by the Prowess Panther system using Monte Carlo simulation. Biomed Phy Engineering Express. 5(5):055005.
18. Shepard DM, Earl MA, Li XA, Naqvi S, Yu C. (2002). Direct aperture optimization: a turnkey solution for step-and-shoot IMRT. Med Phys. 29:1007-1018.
19. Fowler J, Chappell R, Ritter M. (2001). Is alpha/beta for prostate tumors really low? Int J Radiat Oncol Biol Phys. 50(4):1021–1031.
20. Wang JZ, Guerrero M, Li XA. (2003). How low is the alpha/beta ratio for prostate cancer? Int J Radiat Oncol Biol Phys. 55(1):194-203.
21. Cui M, Gao XS, Li X, Ma M, Qi X, Shibamoto Y. (2022). Variability of α/β ratios for prostate cancer with the fractionation schedule: caution against using the linear‑quadratic model for hypofractionated radiotherapy. Radiat Oncol. 17:54
22. Soyfer V, Corn BW, Kollender Y, Tempelhoff H, Meller I, Merimsky O. et al. (2010). Radiation Therapy for Palliation of Sarcoma Metastases: A Unique and Uniform Hypofractionation Experience. Sarcoma. 2010:927972.
23. Elledge CR, Krasin MJ, Ladra MM, Alcorn SR, Han P, Gibbs IC, et al. (2021). A multi-institutional phase 2 trial of stereotactic body radiotherapy in the treatment of bone metastases in pediatric and young adult patients with sarcoma. Cancer. 127(5):739–747.
24. Gutkin PM, Gore E, Charlson J, Neilson JC, Johnstone C, King DM, et al. (2023). Stereotactic body radiotherapy for metastatic sarcoma to the lung: adding to the arsenal of local therapy. Radiat Oncol. 18:42.
25. Fowler J, Yang J, Lamond J, Lanciano R, Feng J, Brady LA. (2010). “Red Shell” concept of increased radiation damage hazard to normal tissues just outside the PTV target volume. Radiother Oncol. 94(3):384.
26. Polan DF, Epelman MA, Wu VW, Sun Y, Varsta M, Owen DR, et al. (2022). Direct incorporation of patient-specific efficacy and toxicity estimates in radiation therapy plan optimization. Med Phys. 49:6279–6292.
27. Ma GC. (2023). Effect of Radiobiological Model Parameterization on Radiotherapy Dose Conversion. Mathews J Cancer Sci. 8(3):44.
28. Steel GG. (2002). Basic clinical radiobiology. 3rd ed. (Oxford University Press Inc., New York, 2002):192-204.